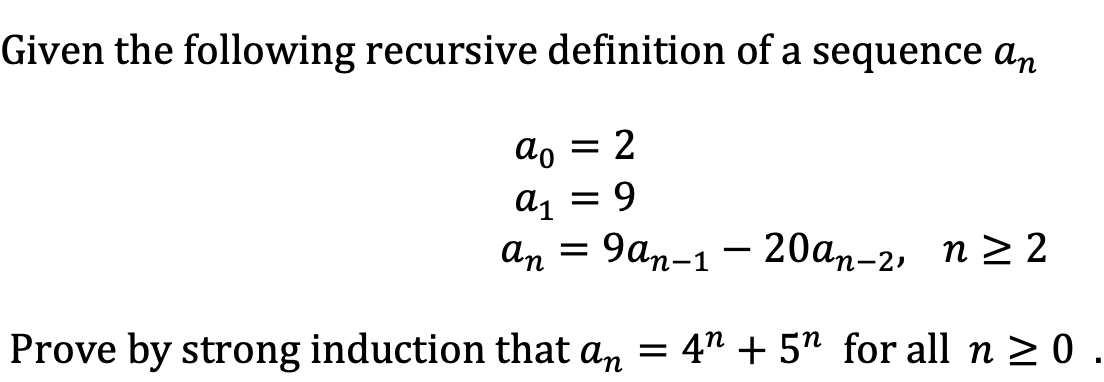UCI ICS/Math 6D5-Recursion -1 Strong Induction “Normal” Induction “Normal” Induction: If we prove that 1) P(n 0 ) 2) For any k≥n 0, if P(k) then P(k+1) - ppt download
How to: Prove by Induction - Proof of a Recurrence Relationship - YouTube
SOLVED: Problem 4 (strong induction - 3 points) If n is a natural number; the number nl, read "n factorial" is the product 1 (n 1) . n, so we have 1! =
SOLVED: Recall that the sequence of Fibonacci numbers fn (n = 0,1,2, V) is defined by the recursive equations fo = 0 fi =1 fn = fn-1 + fn-2 for n >
Solved I'm not sure how to do it but I know that a) should | Chegg.com
Solved 3.Use strong induction. Consider the sequence | Chegg.com
proof writing - Help with induction step of proving a recursive definition / sequence - Mathematics Stack Exchange
real analysis - Help with induction on a recursive sequence. - Mathematics Stack Exchange
Induction and recursion - ppt video online download
SOLVED: Problem (strong induction - 3 points): If n is a natural number, the number n!, read as "n factorial", is the product 1 * 2 * (n - 1) * n.
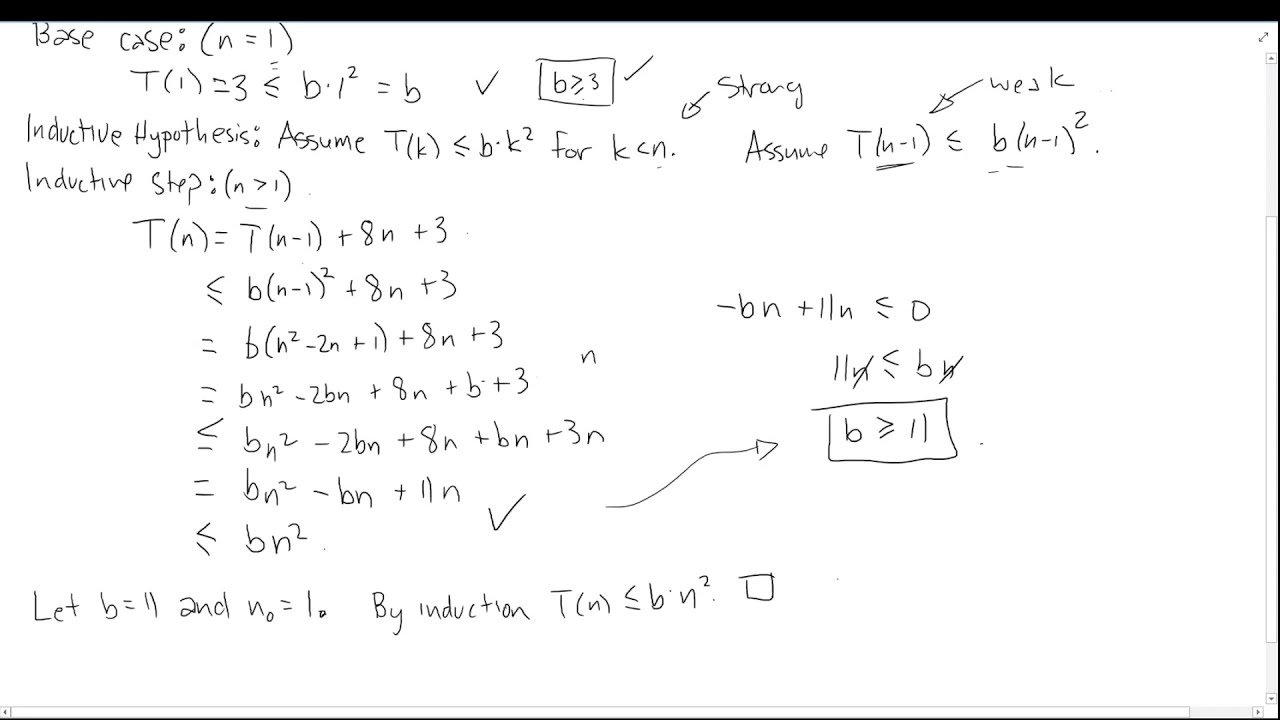
Using strong induction to prove bounds on a recurrence relation - Discrete Math for Computer Science - YouTube
Solved 5. Given the following recursive definition of a | Chegg.com
Mathematical Induction Proof with Recursively Defined Function - YouTube
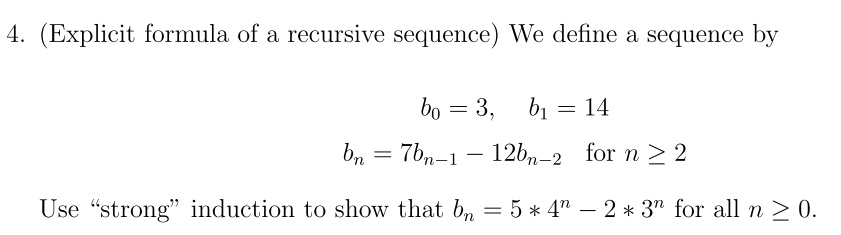
SOLVED: 4 Explicit formula of a recursive sequence) We define a sequence by bo = 3, b1 = 14 bn 7bn-1 12bn-2 for n 2 2 Use "strong" induction to show that bn = 5 * 4" 2 * 3n for all n > 0.
Solved Given the following recursive definition of a | Chegg.com
Answered: Suppose that h, is a sequence… | bartleby
SOLVED: Geometric Sequences. Theory and examples 2.0 Strong Induction. Theory and examples Consider the sequence -1, -1, 3, 7, 11, 15, 19, 23, with a0 = -5. Give a recursive definition for
Strong Induction, Recursive function, Inequality | Sumant's 1 page of Math
How to show that following [math](a_n)[/math]real recursive sequence [math]a_{n + 1} = \dfrac{a_{n}^2 + 2 a_{n} - 3}{a_{n} + 1}[/math] with [math]a_1 = 4[/math] is increasing via mathematical induction? Is this recursive
Mathematical Induction
Proof by Induction: Recursive function with multiple initial terms - YouTube
Proof by Induction - Recursive Formulas - YouTube
Solved 2 Strong Induction Define the sequence b; recursively | Chegg.com
Chapter 4 Induction and Recursion
discrete mathematics - How to find the recursive definition of this function and prove by induction. - Mathematics Stack Exchange
